This set of ALG 4 tasks might require a somewhat greater understanding of algebra than the previous three ALG tasks, if students are to grasp some of the algebraic relations, especially in their more general form. However, even relative novices should be able to engage with the tasks and construe patterns even if this might be at a more empirical level.
MONDAY: This is the root ALG 4 task for this week. It can be approached in quite an exploratory way - later variants become more focused.
Here it is worth dwelling for a while on the form of the three equations, before sketching any lines. Students who know about the form of linear functions may notice that the greater the slope of the corresponding lines, the higher the point of intersection with the y-axis (ie as m increases, so does c, in y = mx + c). In turn this might suggest that the lines are 'hinged' about a common point, which turns out to be the case.
Students without this kind of knowledge can still engage meaningfully with the task, by sketching the lines given by the equations and examining the result.
-
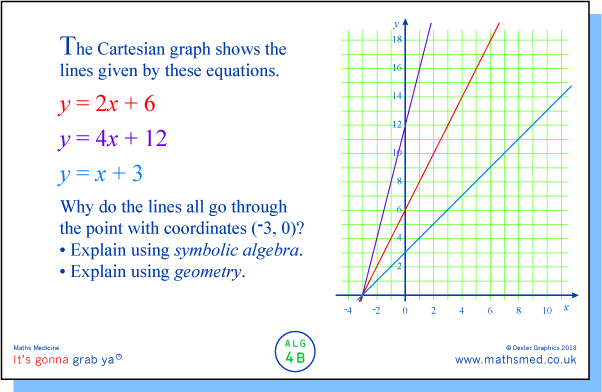
TUESDAY: In this variant we show the three lines and ask students to explain the fact that they go through a common point, using both algebraic and geometric arguments.
As can be seen, the lines all go through the point (-3, 0). We can verify this by letting y = 0 in each of the equations and then solving for x, or by solving for x in the general equation y = ax + 3a or y = a(x + 3) after letting y = 0.
We can also explain this in terms of the slope of the lines and the triangle formed by the points with coordinates (-3, 0), (0, 0) and (0, c). We can think of the slope as being the change in y resulting from a change of +1 in the value of x (below). This means if we increase x by +3, in moving from (-3, 0) to the origin, we increase y by +3×m, and hence cut the y axis at (0, 3m).
-
WEDNESDAY: Here we find the common point for the lines given by another family of equations. But this time, rather than listing individual equations, the family is expressed in a general form. This might help students express the previous family in a similar form if they have not already done so (ie, as y = ax + 3a, as mentioned above). Also, as the two forms are very similar, it might help students see how, and perhaps why, the general form relates to the lines' common point.
[It might be argued that the form y = a(x – 2) is more salient than the given form y = ax – 2a, even though it diverges from the familiar y = mx + c form, as it immediately becomes apparent that x = 2 when y = 0, regardless of the value of a.]
-
THURSDAY: Here we consider another family of equations whose general form, at least at first sight, seems rather different from the form of the two families we've considered so far. It turns out that the common point is not on the x-axis this time.
There are several ways of writing the general form of the family of equations, for example these:
y = ax + (3 – a), y = a(x – 1) + 3, y – 3 = a(x – 1).
What are the affordances of each?
-
FRIDAY: Here we reverse the process, by asking for the family of lines that goes through a specific point.
We can approach this in different ways. One way is to find the equations of some specific lines through (2, 5) and look for a pattern. Another would be to look back at Thursday's task and see what's general about it, ie how does the general equation (in whatever form) relate to the common point?
Another way of thinking about this is to consider lines through the origin (ie of the form y = ax) and to think of translating the lines 2 across and 3 up - how do these steps transform the equation?
An obvious extension of the task would be to consider a general point, with coordinates (u, v), say. If you've managed to solve the task for (2, 5), this should be fairly easy ....