-
MONDAY: A bank holiday and the beginning of school half term in the UK, but that's no reason to deprive ourselves of algebra. Here's our gentle introduction to arithmagons.
We can solve the question 'is there enough flour' by looking at the structure of the problem, which means thinking algebraically. We can take a narrative approach, in this kind of way:
If we add the result of the two weighings, 130 + 160, this is counting the weight of bag A twice, so the total amount of flour is 290 g minus the weight of bag A. So the smaller bag A happens to be, the more flour we've got, and if A weighs 40 g or less, we will have at least 250 g.Or we can express this with symbolic algebra, in this kind of way:
a + b + a + c = 130 + 160 = 290,-
so the total number of grams, a + b + c = 290 – a,
so if a ≤ 40, a + b + c ≥ 250.
TUESDAY: The arithmagon quietly makes an appearance, but we stick with the Peter pancakes story for now. [But it's not pancakes for ever.]
We now know the combined weight for each pair of bags and we look at an approach for hence finding the total weight of the bags - and the weight of any one bag.
NOTE: @ilarrosac (Ignacio Larrosa) has made the interesting observation on Twitter that another context for this problem is to find the radii of three touching circles, given the sum of pairs of radii. A nice thing about this is we can transform the arithmagon triangle into a triangle whose sides are proportional to these sums, in this kind of way (below). This also throws light on the situation where the value of a, b or c turns out to be negative.... as we shall see.
WEDNESDAY: We can relax. The arithmogadon is here.
We are given the same information as in Tuesday's task, namely the value of the sum of each pairing of the three unknown numbers a, b and c. On Tuesday, we found the value of a + b + c (which then allowed us to find the value of each individual unknown) by adding the three pair-sums and halving:
a+b + b+c + c+a = 2(a + b + c), so a + b + c = (130+160+150)÷2 = 220.
This time we use the fact that c must be 30 more than b, and that the sum of b and c is 150, to find c and hence to find a + b + c.
If we are working formally, we can express this information as c = b + 30 and b + c = 150, which we can then combine and transform in this kind of way: c – 30 + c = 150, so 2c = 180, so c = 90.
It is quite possible that these different approaches would have emerged informally as students investigated the original task, so we have now had a chance to make them more explicit.
-
THURSDAY: Here we look at that first scenario again, but in a more systematic way and without the 'real life' context.
We bring out the fact which may well have been noticed in ALG 16A, that the smaller the value of a, the greater the value of the sum a + b + c. [Formally, this can be said to stem from the fact that a+b + a+c = 130+160 = 290 = (a+b+c) + a. And as a increases by 1, the value of a + b + c decreases by 1.]
We also look at the limiting values of a for which the three 'vertices' (a, b and c) are all positive:
when a = 0, b = 130 ans c = 160 and the sum S = a + b + c = 0 + 130+160 = 290;What we haven't done here explicitly is look at the 'permissible' values of the three sums a+b, b+c and c+a, ie the value for which a, b and c are all positive. However, from the previous paragraph we can show that b+c will range from 30 to 290, with, of course, a+b=130 and a+c=160. In effect, the sum of the two smaller sums must be less than or equal to the larger sum - the same condition that applies to the lengths of the sides of a triangle.
when a = 130, b = 0 and c = 30, and S = 130 + 0 + 30 = 160;
note: when a > 130, then b is negative and c is too when a passes 160.
-
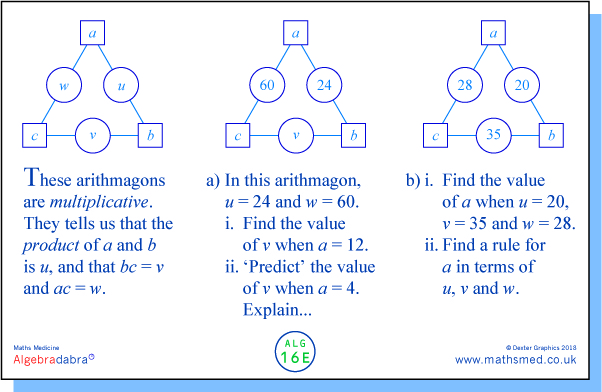
FRIDAY: We switch from an additive to a multiplicative arithmagon. Does Armageddon loom?
Part a) can help us to get a feel for the relationships between the various elements. However, it is quite challenging to pin them down. In b), it is possible to solve part i. by spotting the common factors of u, v, w taken in pairs, though part ii. is likely to prompt one to use formal algebra.
We can solve b)ii using an approach analogous to Tuesday's or Wednesday's approach.
Tuesday's approach: uvw = abbcca = (abc)², so a² = uvw÷v² = uw/v.
Wednesday's approach: u/v = ab/bc = a/c; wu/v = aca/c = a².